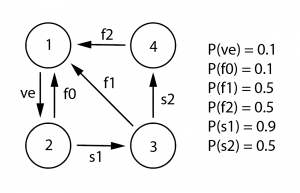
The purpose of this exercise is to practice basic Markov chain calculations for a discrete time, discrete state, finite state example. The Markov chain is a stochastic representation of the distribution grid where the events have the following physical meaning (ve = voltage error; f0 = voltage back to norm without intervention; s1 = first transformer switch; f1 = voltage back to norm following first switch; s2 = second transformer switch; f2 = voltage back to norm following second switch).

Figure 1: Markov chain model

Step 1: Consider the Markov Chain in Figure 1. Is the Markov chain ergodic?

Step 2: In Matlab, define the 1-step probability matrix P.

Step 3: Find the stationary distribution of this Markov chain.

Step 4: Calculate the expected number of steps required to return back to norm following a voltage error.

Step 5: Is the voltage more likely to return back to norm before the second switch?